There are eight equidistant points on a circle. How many right-angled triangles can be drawn using these points as vertices and taking the diameter as one side of the triangle?
This questions was previously asked in
Complete-Test, Previous year (2022)
Explanation:
In the following figure, we have drawn eight equidistant points on a circle - A, B, C, D, E, F, G, and H.
When we consider AE as the diameter and one side of the right-angled triangle, we can draw 6 right-angled triangles.
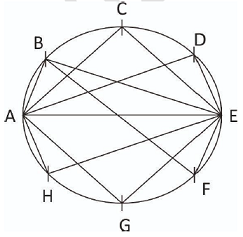
Similarly, we consider BF as the diameter and one side of the right-angled triangle, we can draw 6 right-angled triangles.
We can do the same when we consider CG and DH as the diameter and one side of the right-angled triangle.
Hence, the total number of right-angled triangles that can be drawn = 6 + 6 + 6 + 6 = 24
![]()
By: Munesh Kumari