95% of the students in a class have taken Marketing, 80% have chosen Finance, 84% have chosen operations (ops), and 90% have chosen Human Resources (HR). What is the maximum and minimum percentage of people who have chosen all of the four?
80% and 56%
Incorrect Answer95% and 53%
Incorrect Answer80% and 49%
Correct Answer80% and 51%
Incorrect AnswerExplanation:
Finding the maximum percentage is easy.
If F ⊂ O ⊂ H ⊂ M , then the percentage of people who have taken all 4 should be 80% and this is the maximum value it can take.
For the value to be minimum, the numbers should be as far ‘apart´ as possible. Let us do this iteratively.
First, let us take Marketing and Finance, and see if we can find the minimum percentage of students who should have taken both.
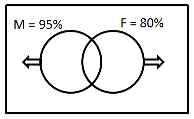
When M and F, are as far ‘apart´ as possible, M ∩ F would be minimum. And the minimum value would be 80% + 95% – 100% = 75%.
Now, let us start with this M ∪ F and add Ops to the mix.
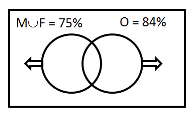
Now, the minimum value of M ∩ F ∩ O would be when these are as far ‘apart’ as possible.
And the minimum value would be 75% + 84% – 100% = 59%.
Adding HR also to the mix, we get -
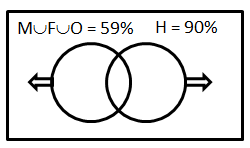
The minimum possible value of M ∩ F ∩ O ∩ H = 59% + 90% – 100% = 49%.
As a formula, the minimum value is 100% – (100% – 95%) – (100% – 80%) – (100% – 84%) – (100% – 90%).
= 100% – 5% – 20% – 16% – 10% = 100% – 51% = 49%.
Again, do not go with just the formula. See the trial and error iteration.
The trial and error iteration is far more useful than knowing the formula for a template.
Hence, the answer is "80% and 49%".
![]() By: Amit Kumar
By: Amit Kumar