There are 9 cups placed on a table arranged in equal number of rows and columns out of which 6 cups contain coffee and 3 cups contain tea. In how many ways can they be arranged so that each row should contain at least one cup of coffee?
This questions was previously asked in
Complete-Test, Previous year (2022)
Explanation:
The cups will be arranged in a 3 × 3 matrix.
Now, let’s consider all the possible cases.
Case 1: Each row has 2 cups of coffee and 1 cup of tea.
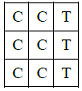
One tea cup can be placed in a row in 3 ways.
So, Possible arrangements wherein all rows have 2 coffee cups= 3×3×3 = 27 ways
Case 2: One row has 3 cups of coffee.
In such a case, one of the rows will have 2 cups of coffee and the other will have 1 cup of coffee.

If the first row has 3 coffee cups, then the possible arrangements = 3×3 = 9 ways
The rows having 3, 2 and 1 coffee cups can be arranged in 3! = 6 ways
So, Possible arrangements wherein one row has 3 coffee cups = 9 × 6 ways = 54 ways
Therefore, total possible arrangements = 27 + 54 = 81 ways
Hence, option (d) is the correct answer.
![]() By: Munesh Kumari
By: Munesh Kumari